矩形和菱形的判定（矩形和菱形的判定依据）

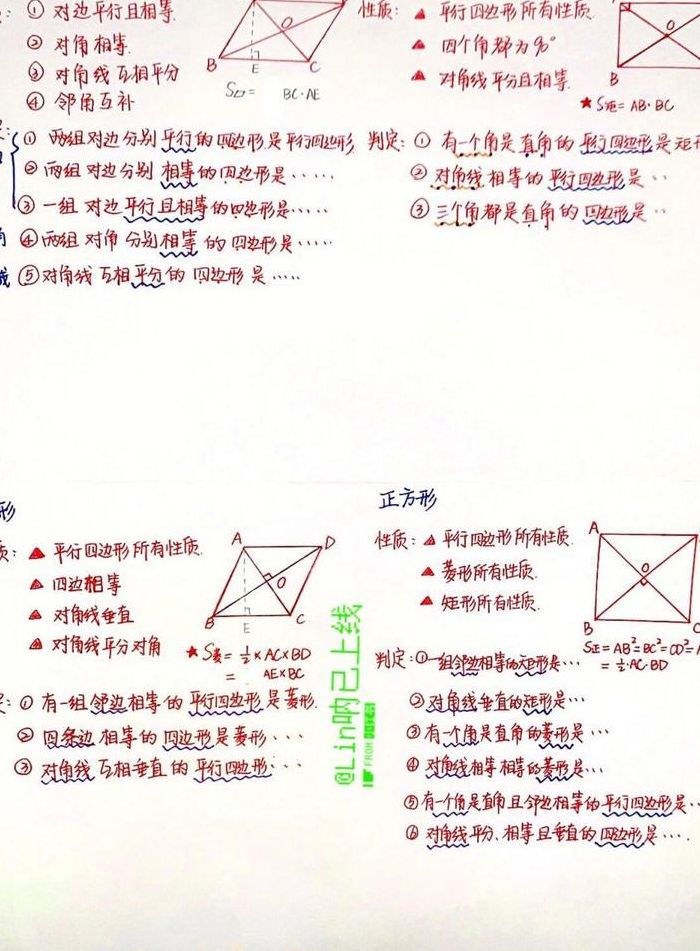
求平行四边形,矩形,菱形的判定定理和性质定理

平行四边形的判定包括：1）两组对边分别平行的四边形；2）两组对边分别相等的四边形；3）一组对边平行且相等的四边形；4）两组对角分别相等的四边形；5）对角线互相平分的四边形。这些条件中的任意一个都可验证一个四边形是否为平行四边形。

菱形是轴对称图形，对角线所在的直线是它的对称轴。判定定理：一组邻边相等的平行四边形是菱形。对角线互相垂直平分的平行四边形是菱形。四条边都相等的四边形是菱形。

有一组邻边相等的平行四边形叫做菱形。四边都相等的四边形是菱形。对角线互相垂直的平行四边形是菱形。正方形性质：正方形具有四边形、平行四边形、矩形、菱形的一切性质。正方形的判定方法：先证它是矩形，再证有一组邻边相等或对角线垂直。

矩形判定方法：三个角是直角的四边形是矩形。一个内角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。正方形判定方法：只要证明该四边形同时是平行四边形，菱形，矩形就可以了。上述方法之一任选几个就可以证明，方法比较多。

依次连接四边形各边中点所得的四边形称为中点四边形。不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形。正方形的中点四边形是正方形。

有三个角是直角的四边形是矩形 对角线相等的平行四边形是矩形 有一个内角是直角的平行四边形是矩形 菱形判定定理 ① 四条边相等的四边形是菱形 ② 对角线互相垂直的平行四边形是菱形 ③ 一组邻边相等的平行四边形是菱形 ④对角线互相垂直且平分的四边形是菱形。等腰三角形 底角相等。两边相等。

矩形,菱形,正方形的判定方法有哪些?

矩形：（在平行四边形基础上）有一角为直角；对角线相等。菱形：（在平行四边形基础上）有一组邻边相等；对角线垂直；对角线也是角平分线。

正方形的判定方法包括对角线相等且互相垂直的菱形，对角线互相垂直的矩形，对角线互相垂直平分且相等的四边形，一组邻边相等且有三个角为直角的四边形，以及一组邻边相等的矩形。平行四边形定义为在同一平面内有两组对边分别平行的四边形。

菱形：平面内，一个四边形任意一条都与它的对边平行，且它的4条边长相等。梯形：平面内，一个四边形有且只有两条边互相平行。矩形：平面内，四个内角都是90°的四边形 正方形：平面内，四个内角都是90°，且4条边长相等的四边形。

平行四边形有一组邻边相等时就是菱形，菱形的对角线相等时就是正方形。判定定理 1：对角线相等的菱形是正方形。2：有一个角为直角的菱形是正方形。3：对角线互相垂直的矩形是正方形。4：一组邻边相等的矩形是正方形。5：一组邻边相等且有一个角是直角的平行四边形是正方形。

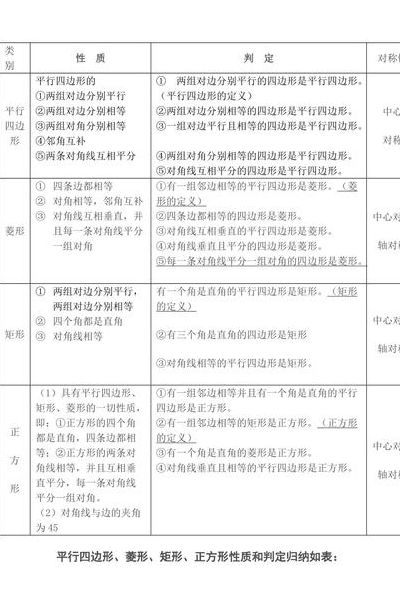
平行四边形,矩形,菱形,正方形的定义和判定方法?要求:表格形式

平行四边形：两对边分别相等；两对角分别相等；两对边分别平行；有一组对边平行且相等；对角线互相平分。矩形：（在平行四边形基础上）有一角为直角；对角线相等。菱形：（在平行四边形基础上）有一组邻边相等；对角线垂直；对角线也是角平分线。

一组邻边相等的平行四边形是菱形。对角线互相垂直的平行四边形是菱形。四边相等的四边形是菱形。矩形：三个角是直角的四边形是矩形。一个内角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形。正方形：对角线相等的菱形是正方形。有一个角为直角的菱形是正方形。

判定：四条边都相等的四边形，对角线互相垂直的平行四边形。正方形 定义：有一组灵便相等且有一个角是直角的平行四边形 性质：四条边相等，四个角都是直角，对角线相等，且互相平分，每个叫平分一组对角。

正方形的判定方法包括对角线相等且互相垂直的菱形，对角线互相垂直的矩形，对角线互相垂直平分且相等的四边形，一组邻边相等且有三个角为直角的四边形，以及一组邻边相等的矩形。平行四边形定义为在同一平面内有两组对边分别平行的四边形。

菱形：对边平行，四条边都相等，对角相等，两条对角线互相垂直平分，每条对角线平分一组对角，轴对称，中心对称。 正方形：对边平行且四边都相等，四个角都是直角，两条对角线互相平分且相等，每条对角线平分一组对角，轴对称，中心对称。

正方形 定义：在同一平面内四条边都相等且一个角是直角的四边形叫做正方形。有一组邻边相等的矩形是正方形。有一组邻边相等且垂直的平行四边形是正方形。有一个角为直角的菱形是正方形。

The End