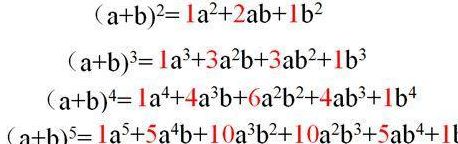二项式展开公式（广义二项式展开公式）

二项式的展开式是什么?

即（a+b）的n次展开式 性质 在二项展开式中，与首末两端等距离的两项系数相等。如果二项式的幂指数是偶数，中间的一项系数最大。如果二项式的幂指数是奇数，中间两项的系数最大，并且相等。

二项展开式是依据二项式定理对(a+b)n进行展开得到的式子，由艾萨克·牛顿于1664-1665年间提出。二项展开式是高考的一个重要考点。在二项式展开式中，二项式系数是一些特殊的组合数，与术语“系数”是有区别的。

二项式乘方展开，又叫二项式公式，是初等数学中的一个最基本的公式。

二项展开式公式

(a+b)^n=a^n+[C(n，1)]a^(n-1)*b+C(n，2)a^(n-2)b^2+……+C(n-1，n)ab^(n-1)+b^n通项T(k+1)=C(n，k)a^(n-k)*b^k。

二项式展开公式：(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n 二项展开式是依据二项式定理对(a+b)n进行展开得到的式子。

即为（a+b）n次方的展开式，称为二项展开式。

二项式定理展开式公式是什么?

二项展开式的通项公式(简称通项)为C（n，r）(a)^(n-r)b^r，用Tr+1表示(其中r+1为角标)，即通项为展开式的第r+1项(如下图)，即n取i的组合数目。因此系数亦可表示为杨辉三角或帕斯卡三角形。

二次项定理展开式：Tr+1=Cn^r*a^n-rb^r 二次项定理，又称为牛顿二项式定理。它是由艾萨克·牛顿于1665年发现的。

(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n。二项式定理（英语：Binomial theorem），又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年期间提出。

n，1)a^(n-1)b++C(n，r)a^(n-r)b^r++C(n，n)b^n 二项式定理可以用以下公式表示： 其中， 又有 等记法，称为二项式系数，即取的组合数目。此系数亦可表示为杨辉三角形。[2] 它们之间是互通的关系。

二项式展开公式：(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n。

二项式定理又称：二项式展开式，是一种数学公式，它包含了各种可能的组合，并给出了每个组合的结果。

二项式定理的展开公式是什么?

1、二项展开式的通项公式(简称通项)为C（n，r）(a)^(n-r)b^r，用Tr+1表示(其中r+1为角标)，即通项为展开式的第r+1项(如下图)，即n取i的组合数目。因此系数亦可表示为杨辉三角或帕斯卡三角形。

2、二次项定理展开式：Tr+1=Cn^r*a^n-rb^r 二次项定理，又称为牛顿二项式定理。它是由艾萨克·牛顿于1665年发现的。

3、二项展开式是依据二项式定理对(a+b)^n进行展开得到的式子，由艾萨克·牛顿于1664-1665年间提出。二项展开式是高考的一个重要考点。在二项式展开式中，二项式系数是一些特殊的组合数，与术语“系数”是有区别的。

4、二项展开式的通项公式是T（r+1）=C（n，r)a^(n-r)b^rT（r+1）。

5、二项式定理的公式为：（a+b）^n=Σ（i从0到n）C（n，i）*a^i* b^（n-i），其中C（n，i）表示组合数，即从n个不同元素中选取i个元素的组合数。这个公式的证明可以通过数学归纳法或者利用多项式定理来进行。

6、二项式展开公式：(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n。

二项展开式的公式是什么?

二项式展开公式：(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n 二项展开式是依据二项式定理对(a+b)n进行展开得到的式子，由艾萨克·牛顿于1664-1665年间提出。

二项式展开公式：（a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n。

即为（a+b）n次方的展开式，称为二项展开式。

二项展开式的通项公式是T（r+1）=C（n，r)a^(n-r)b^r T（r+1）表示二项展开式的第r+1项，C（n，r)表示n个数中取r个数的组合^表示次方，表示后面的数是前面的数的上标次方的意思。

二项式定理展开式公式

二项式展开公式：(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n 二项展开式是依据二项式定理对(a+b)n进行展开得到的式子。

(a+b)^n=a^n+C(n，1)a^(n-1)b+C(n，2)a^(n-2)b^2+...+C(n，n-1)ab^(n-1)+b^n。二项式定理（英语：Binomial theorem），又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年期间提出。

二项式定理（英语：binomial theorem），又称牛顿二项式定理，由艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂，即广义二项式定理。

二项展开式的通项公式(简称通项)为C（n，r）(a)^(n-r)b^r，用Tr+1表示(其中r+1为角标)，即通项为展开式的第r+1项(如下图)，即n取i的组合数目。因此系数亦可表示为杨辉三角或帕斯卡三角形。

二项式定理可以用如下公式表示：常数项 二项式展开式中的常数项，指的是使得a^(n-r)b^r次方为常数，不包含未知变量。考试中较常出现的二项式展开式中常数项的系数求法，就是用到这个原理。

The End