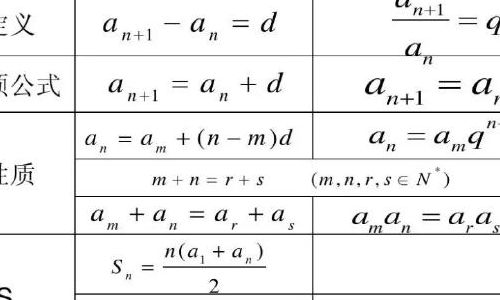等差数列通项公式
等差数列基本公式: 末项=首项+(项数-1)*公差 项数=(末项-首项)÷公差+1 首项=末项-(项数-1)*公差 和=(首项+末项)*项数÷2 末项:最后一位数 首项:第一位数 项数:一共有几位数 和:求一共数的总和。
等差数列的通项公式为:an=a1+(n-1)d 前n项和公式为:Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (n属于自然数)。a1为首项,an为末项,n为项数,d为等差数列的公差。
公差为d的等差数列{an},当n为奇数时,等差中项为一项,即等差中项等于首尾两项和的二分之一,也等于总和Sn除以项数n,将求和公式代入即可。当n为偶数时,等差中项为中间两项,这两项的和等于首尾两项和,也等于二倍的总和除以项数n。
等差数列通项公式:an=a1+(n-1)*d,其中n是项数。另外,若首项a1=1,公差d=2。前n项和公式为Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。注意,以上n均属于正整数。等差数列是指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。
等差数列{an}的通项公式为:an=a1+(n-1)d、an=am+(n-m)d。等差数列前n项和公式:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。
等差数列的通项公式是啥?
1、等差数列的通项公式为:an=a1+(n-1)*d,首项a1=1,公差d=2。通项公式推导:a2-a1=d;a3-a2=d;a4-a3=d……an-a(n-1)=d,将上述式子左右分别相加,得出an-a1=(n-1)*d→an=a1+(n-1)*d。
2、等差数列基本公式: 末项=首项+(项数-1)*公差 项数=(末项-首项)÷公差+1 首项=末项-(项数-1)*公差 和=(首项+末项)*项数÷2 末项:最后一位数 首项:第一位数 项数:一共有几位数 和:求一共数的总和。
3、等差数列的通项公式为:an=a1+(n-1)d 前n项和公式为:Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (n属于自然数)。a1为首项,an为末项,n为项数,d为等差数列的公差。
怎样求等差数列的通项公式?
等差数列的所有公式如下:等差数列{an}的通项公式为:an=a1+(n-1)d、an=am+(n-m)d。等差数列前n项和公式:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。
等差数列的前n项和公式表示为:Sn=n/2(a1+an)其中,Sn表示等差数列的前n项和,a1表示等差数列中第一项,an表示等差数列中第n项。公差公式 公差d是等差数列中任意两项之间的差,因此d的公式为:d=an-an-1 其中,an表示等差数列中第n项,an-1表示等差数列中第n-1项。
等差数列的公式:公差d=(an-a1)÷(n-1)(其中n大于或等于2,n属于正整数)。项数=(末项-首项来)÷公差+1。末项=首项+(项数-1)×公差。前n项的和Sn=首项×n+项数(项数-1)公差/2。第n项的值an=首项+(项数-1)×公差。
等差数列的通项公式是什么?
等差数列基本公式: 末项=首项+(项数-1)*公差 项数=(末项-首项)÷公差+1 首项=末项-(项数-1)*公差 和=(首项+末项)*项数÷2 末项:最后一位数 首项:第一位数 项数:一共有几位数 和:求一共数的总和。
等差数列的通项公式为:an=a1+(n-1)d 前n项和公式为:Sn=na1+n(n-1)d/2或Sn=n(a1+an)/2 (n属于自然数)。a1为首项,an为末项,n为项数,d为等差数列的公差。
公差为d的等差数列{an},当n为奇数时,等差中项为一项,即等差中项等于首尾两项和的二分之一,也等于总和Sn除以项数n,将求和公式代入即可。当n为偶数时,等差中项为中间两项,这两项的和等于首尾两项和,也等于二倍的总和除以项数n。
等差数列{an}的通项公式为:an=a1+(n-1)d、an=am+(n-m)d。等差数列前n项和公式:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。
等差数列 指从第二项起,每一项与它的前一项的差等于同一个常数的一种数列,常用A、P表示。这个常数叫做等差数列的公差,公差常用字母d表示。例如:1,3,5,7,9……2n-1。通项公式为:an=a1+(n-1)*d。首项a1=1,公差d=2。前n项和公式为:Sn=a1*n+/2或Sn=/2。
文章声明:以上内容(如有图片或视频亦包括在内)除非注明,否则均为网友提供或互联网,转载或复制请以超链接形式并注明出处。