等边三角形的面积（等边三角形的面积和边长的关系）

等边三角形面积是多少?

1、等边三角形都面积为S= (√3)a/4，a为边长，s为面积。

2、等边三角形面积公式为：S=(√3)a/4，（S是三角形的面积，a是三角形的边长）。推断过程：等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。

3、等边三角形为三边相等的三角形，其三个内角相等，均为60°，如果等边三角形的边长为a，那么它的高为√a/2，等边三角形的面积为1/2a^2sin60°=√3/4a^2。三角形角的性质：在平面上三角形的内角和等于180°（内角和定理）。在平面上三角形的外角和等于360° (外角和定理)。

4、等边三角形面积是（根号3/4）*（边长的平方），公式即S=（(√3)/4）a。

5、小学数学中，计算等边三角形的面积可以使用公式：面积=(边长^2*√3)/4。拓展知识：等边三角形是指三个边长都相等的三角形。在小学数学中，计算等边三角形的面积是一个基本的几何问题。下面将按照序号标题的方式详细描述计算等边三角形面积的方法。

等边三角形面积公式

1、等边三角形面积的计算公式：S=√3/4a。等边三角形的边长为a。边长公式：C=3a。等边三角形，为三边相等的三角形，其三个内角相等，均为60°。

2、如果等边三角形的边长为a 那么它的高为√a/2 所以等边三角形的面积公式：等边三角形与圆的有关计算公式：高： ；内切圆半径： ；外接圆半径：； ；表示内切圆面积， ；表示外接圆面积。由此可知等边三角形外接圆面积是内切圆面积的4倍。

3、等边三角形面积的计算公式： S=√3/4a 。等边三角形的边长为a 。边长公式： C=3a。等边三角形的性质 （1）等边三角形是锐角三角形，等边三角形的内角都相等，且均为60°。（2）等边三角形每条边上的中线、高线和角平分线互相重合。

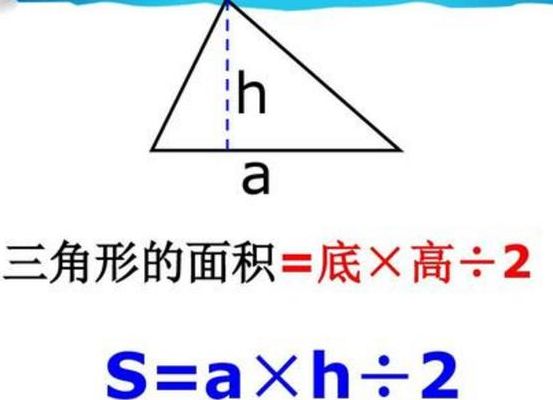
4、奠基知识：S普通△＝1/2ah（底×高÷2）推理解析：要推理等边三角形面积公式，就要从普通三角形面积公式开始。由普通三角形的底×高÷2，得出等边三角形的底×高÷2，但在这里就要发挥等边三角形的特殊性。

5、等边三角形面积是（根号3/4）*（边长的平方），公式即S=（(√3)/4）a。

6、等边三角形面积公式为：S=(√3)a/4，（S是三角形的面积，a是三角形的边长）。推断过程：等边三角形（又称正三边形），为三边相等的三角形，其三个内角相等，均为60°，它是锐角三角形的一种。等边三角形也是最稳定的结构。

等边三角形的面积怎么计算?

等边三角形为三边相等的三角形，如果等边三角形的边长为a，那么它的高为√a/2，等边三角形的面积为1/2a^2sin60°=√3/4a^2。等边三角形是特殊的等腰三角形，所以等边三角形拥有等腰三角形的一切性质。

解：边长为a的等边三角形面积公式 S=√3a/4 所以，这个三角形的面积 =9√3/100 如仍有疑惑，欢迎追问。

三角形2条边为5米，底边为5米，是等腰三角形。

等边三角形面积是（根号3/4）*（边长的平方），公式即S=（(√3)/4）a。

欧几里得的方法是将等边三角形分成两个相等的直角三角形，每个直角三角形的面积是底边长的2分之1乘以高，因此等边三角形的面积是两个直角三角形面积的和，即底边长的2分之1乘以高的2分之1乘以2。

算等边三角形的面积的方法如下：等边三角形是一种特殊的三角形，其三条边的长度相等。等边三角形的面积计算公式是：面积 = (边长 × 边长 × √3) ÷ 4。这个公式是基于等边三角形的性质和几何定理推导出来的。

等边三角形面积公式是什么

1、等边三角形面积的计算公式：S=√3/4a。等边三角形的边长为a。边长公式：C=3a。等边三角形，为三边相等的三角形，其三个内角相等，均为60°。

2、所以等边三角形的面积公式：等边三角形与圆的有关计算公式：高： ；内切圆半径： ；外接圆半径：； ；表示内切圆面积， ；表示外接圆面积。由此可知等边三角形外接圆面积是内切圆面积的4倍。

3、等边三角形面积公式：S=（（√3）/4）a（a为三角形的边长）。分析过程如下：在上诉求等边三角形面积的时候，用到了勾股定理以及三角形的面积公式：三角形的面积=底×高÷2。运用等边三角形的三线合一，底边上的高垂直平分底边，求出底边上的高，再根据角形的面积=底×高÷2。

4、等边三角形面积公式为：面积 = 高等乘底除2。等边三角形 等边三角形是一种特殊的三角形，它的三条边长都相等，三个角度也都相等，每个角度都是60度。等边三角形的特性 三条边长都相等，任意两条边长之间的距离都相等。三个角度都相等，都是60度。

5、已知等边三角形边长，三角形的面积：假设等边三角形的边长为a，等边三角形的高为：asin60°，由此可计算出该等边三角形的面积为：（1/2）*a*a*sin60°=asin60°/2。

The End