快速算术（快速算术法）

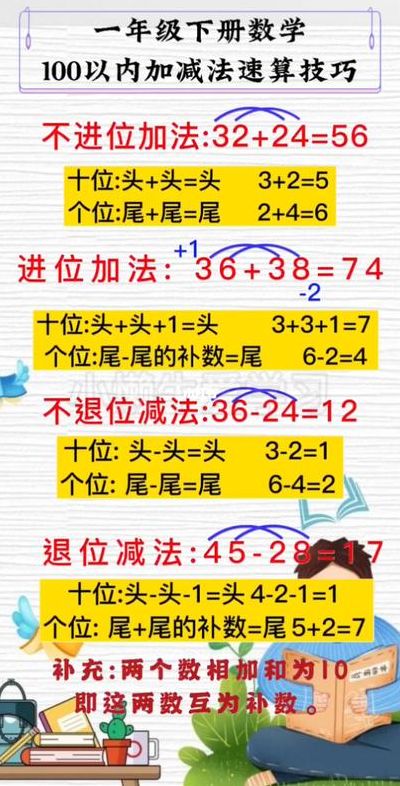
练习速算有哪些技巧?

1、两位数速算方法与技巧有熟练掌握加法、减法运算、乘法运算、除法运算。加法速算 十位上相加，个位上相加，若有进位则补到十位上。67+25=92，6+2=8，7+5=12，进位，最终结果为92。把两个数都变成离它们最近的整十数，再相加，最后再加上多出来的数。

2、小学数学速算方法与技巧 改变运算顺序：在只有“+”、“-”号的混合算式中，运算顺序可改变。计算等差连续数的和相邻的两个数的差都相等的一串数就叫等差连续数，又叫等差数列。等差连续数的个数是偶数时，它们的和等于首数与末数之和乘以个数的一半。

3、乘法速算：乘法速算通用公式：abcd=(a+1)c100+bd+魏氏速算嬗数10。速算嬗数|=(a-c)d+(b+d-10)c，速算嬗数‖=(a+b-10)c+(d-c)a，速算嬗数Ⅲ=ad-b(补数)c 。

幼儿快速加减算术技巧

1、画图法可以让小宝宝一目了然地计算出简单的加减法，可以说是最简单的加减法计算方法。图片法可以制作一些特别漂亮的图片，让这些图片代表不同的数字，这样就可以调动孩子学习的积极性，同时可以非常简单的就可以看出加减法到底应该如何计算。

2、在纸上画出简单的树棍，通过移动和组合这些树棍，孩子们可以直观地看到加减法的结果。手指法手指法是一种寓教于乐的方法。孩子们可以用手指代表数字，通过简单的加减动作来理解和计算加减法，既有趣又实用。凑十法凑十法是一种高效的计算方法。

3、方法：在一个加式里，如果被加数或加数有一个接近整整百、整千等，都以整数来加，然后再减去这个差数（即补数），这样计算起来十分方便。幼儿加减法手指速算 口诀：用第一个加数加上第二个加数的整整百、整千……再减去第二个加数与整整百、整千……的差，等于和。

4、在教孩子加减法时，可以从简单的加减法开始，比如1+1=2，2-1=1。等孩子掌握了简单的加减法后，再逐渐增加难度。 结合实物操作 孩子的学习方式是形象思维，因此在教孩子加减法时，可以结合实物操作，让孩子更容易理解。比如，可以让孩子用积木、玩具等来演示加减法。

5、怎样让小孩快速算加减法1 画图法。可以将加减法转变成为画图法，让孩子通过画图，这样直观的看出加减法到底应该如何计算。画图法可以让小宝宝一目了然地计算出简单的加减法，可以说是最简单的加减法计算方法。图片法。

6、加减位置是：一位数十位加减，两位数百位加减。如：35×28＝980，计算程序是：(3＋1)×2＝8，5×8＝40，相连为840，这不是应求的 积数，还有两比，一是比首，3比2大1，就要加一个乘数尾，加8，二是比尾，5＋8＝13，13比10大3，就加3个乘数首，3×2＝6，8＋6＝14，两位数百位加，840＋140＝980。

怎么教孩子100以内快速计算

以内的数，可以把它分成几类，在儿子能接受的基础上分类较好，每类熟练后再教下一类。口算基础口算，其实就是在不断练习的基础上，养成一种算的习惯，这需要反复练习。

凑整加法就是凑整加差法，先凑成整数后加差数，就能算的快。8+7=15 计算时先将8凑成10 8加2等于10 7减2等于5 10＋5=15 如17＋9=26 计算程序是17+3=20 9-3=6 20+6=26 二 .补数加法 补数加法速度快，主要是没有逐位进位的麻烦。补数就是两个数的和为10 100 1000 等等。

幼儿数数1-100的第三阶段就是在10-20的基础上，给孩子讲解数的形式规律，这样就方便他们记忆了。而此时也要利用各种实物的操作来提高孩子对十进制的认知能力，这样才能真正地学会数数，并且知道每个数代表的含义。

可以搭配一些简单的识数玩具帮助教学，利用玩具可以让宝宝对数字产生兴趣，并且可以更加形象地识数。单纯的学习识数很容易让孩子感到枯燥。因此，家长最好也叫上孩子的朋友或者同学一起学习，两个人可以互相学习进步。

两位数加两位数的进位加法 口诀：加9要减1，加8要减2，加7要减3，加6要减4，加5要减5，加4要减6，加3要减7，加2要减8，加1要减9。

第 首先，我们应该给孩子打下一个良好的基础，这就要求我们在孩子上幼儿园的时候，或者在平时在家的时候我们就有意识地引导孩子去学习算数。第 平时家里买了芋头或者其他食物的时候我们也可以教孩子进行数数，这样子孩子最初可以对数字有一个概念，在学会数数以后就可以教她如何进行加减了。

快速计算数学的方法

1、提取公因式 这个方法实际上可以理解为乘法分配律逆向变化，将相同因数提取出来，考试中往往剩下的项相加减（各个数前面的符号各自带着），然后会出现一个整数，计算起来就要方便得多。注意相同因数的提取。

2、大数相乘 例如，计算7×531，尽可能地拆散数字为100等等的倍数。乘以12 将被乘数乘以10，然后将其相加两次，然后将这些数字相加即可得出答案。关于15%的计算 如果想计算一个数字的15％，首先需要算出10％。让我们以400为例。将小数点向左移动一位。然后将该数字除以2，结果加40。

3、操作方法：利用运算定律。利用加法的交换律和结合律，乘法的交换律、结合律和分配律，可以使计算简便。分解因数。有的特殊数相乘是可以得到整数的，比如25和4，125和8等等，在我们遇到这些数字时，可以想办法把它们变成能得到整数的数字。数字变形。

4、快速心算方法有珠算式心算、记忆数字规律、数学技巧等。珠算式心算：这种方法是通过模拟算盘来提高心算速度。通过熟练的练习，可以将算盘的运作过程转化为内心的计算过程，从而快速得出答案。珠算式心算需要大量的练习和技巧，但一旦掌握，可以大大提高计算速度。

5、除法：* 对于多位数的除法，可以利用竖式除法进行计算。* 可以利用估算的方法进行快速计算。此外，还可以通过以下方法来提高计算速度：* 经常练习，熟能生巧。* 集中注意力，减少计算过程中的错误。* 保持良好的心态，不要因为计算而感到焦虑。

6、头互补、尾相同的速算方法：对于两个数的十位数互补、个位数相同的数字相乘，可以简化计算过程。例如：67×47，两个数字的十位数分别是6和4，个位数都是7。可以将两个数分别转化为60+7和40+7，然后直接相乘得到结果。

凑十法和借十法:快速算数的好方法

1、“减九加一”的借数歌：看到9想到1，看到8想到2，看到7想到3，看到6想到4，大数减小数，差了几个就借几。“减八加二”的补数歌：看到8想到2，看到7想到3，小减大来算相差，比着大的往前排。“减七加三”的拆数歌：看到7想到3，看到9想到1，拆大补小算相差，比着大的往前排。

2、一加九，十只小蝌蚪。二加八，十只花老鸭。三加七，十只老母鸡。四加六，十只金丝猴。五加五，十只大老虎。凑十法口诀 一凑九，二凑八，三凑七，五五相凑就满十。凑十法口诀 看到9想到1，看到8想到2，看到7想到3，看到6想到4。看到大数加小数，先把两数换位置。

3、二八二八手拉手【8】三七三七真亲密【7】四六四六一起走【6】五五五五一双手【5】凑十法是20以内进位加法的基本思路。运用凑十法能将20以内的 进位加法转化为学生所熟悉的10加几的题目，从而化难为易。

4、凑9/：如9+8，8拆为1和7，1+9=10，进位至十位，得到1 5凑5/：5+7，7拆为5和2，5+5=10，所以5+7=1 每一步都如同搭建积木，熟练后，每个数字间的组合都能迅速在脑海中形成清晰的图像，算数难题瞬间迎刃而解。

5、“借十法”帮助学生将复杂的减法问题转化为更简单的10减去几的形式。例如，对于35-8的计算，可以将35分解为25和10，先用10减去8得到2，再用25加上2，即可得到结果。凑十法 “凑十法”是处理20以内进位加法的有效方法。

6、破十法凑十法借十法平十法口诀如下：首先，凑十法是指通过将两个数相加或相减，使结果接近或等于十的方法。这个方法可以帮助学生在心算过程中更加灵活和准确。例如，当学生计算8+5时，他们可以使用凑十法，将8凑成10，再加上剩下的2，最后得到的结果是10+2=12。

除法的快速计算法

逆运算法：说明：当知道除数和某个与被除数接近的数的除法结果时，可以通过乘法和加法或减法来估算被除数的除法结果。例子：将348除以12。大家知道12乘以25等于300，这与348非常接近。现在，只需要将348减去300得到48。大家知道4乘以12等于48，所以最终的商是25+4=29。

除法的速算与巧算如下：个位数是“1”。速算口诀：头乘头，头加头，尾是1(头加头如果超过10要进位)。十位数是“1。速算口诀：头是1，尾加尾，尾乘尾(超过10要进位)。个位数都是“9”。速算口诀：头数各加1，相乘再乘10，减去相加数，后再放1。十位数都是9”。

约分法 约分法也是一种快速计算除法的方法。当除数和被除数都可以被同一个数整除时，我们可以将除数和被除数同时约分，然后进行计算。例如，计算24÷6，我们可以发现24和6都可以被2整除，因此可以将24和6同时除以2，得到24÷6=4。竖式法 竖式法是除法运算中常用的一种计算方法。

除法的计算小技巧如下：小位数：凡是被除数含有除数3倍时，其方法为：被除数含商1倍：由本位加补数一次。被除数含商2倍：由本位加补数二次。被除数含商3倍：由本位加补数三次。

理解除法与乘法的互逆关系：除法和乘法是互为逆运算的。例如，如果8÷4=2，那么也可以写成4×2=8。这是因为分配4个苹果给每个人可以得到8个苹果。使用整除法解题：对于一些简单的除法问题，可以使用整除法来快速找到答案。例如，如果一个数能被另一个数整除，那么这个数就是它们的商。

四舍五入法 四舍五入法试商也是分类的，简单些的就是我们课内学习的，把除数看作和它接近的整十数去试商，像96÷32，把32看成30去试商，商3就可以了，如果被除数的前两位比除数小，就用前三位除以除数。比如192÷39。

The End