勾股定理的证明（勾股定理的证明方法12种）

勾股定理的5种证明方法

相似三角形法：利用相似三角形的性质，证明勾股定理。矩形法：将一个直角三角形内切于一矩形中，从而证明勾股定理。差积公式法：利用差积公式（a+b）（a-b）=a-b，证明勾股定理。面积法：利用直角三角形的两条直角边构成一个矩形，证明勾股定理。

勾股定理5种证明方法如下：几何法证明：使用几何图形的性质来证明勾股定理。应用勾股定理法证明：使用已知的勾股定理来证明勾股定理。斜率法证明：使用斜率的定义来证明勾股定理。三角函数法证明：使用三角函数的性质来证明勾股定理。欧拉定理法证明：使用欧拉定理来证明勾股定理。

勾股定理五种证明方法带图有课本证明，赵爽弦图证明等。证法一（课本的证明）：如上图所示两个边长为a+b的正方形面积相等，所以a^2+b^2+4（1/2）ab=c^2+4（1/2）ab，故a^2+b^2=c^2。

这也是一种证明勾股定理的方法，而且也很简洁。它利用了相似三角形的知识。在对勾股定理为数众多的证明中，人们也会犯一些错误。如有人给出了如下证明勾股定理的方法：设△ABC中，∠C=90°，由余弦定理 c2=a2+b2-2abcosC，因为∠C=90°，所以cosC=0。所以 a2+b2=c2。

勾股定理的证明方法

1、几何法：构造一个直角三角形，利用勾股定理求出斜边长。代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。数学归纳法：证明当斜边长为n时，勾股定理成立，再证明当斜边长为n+1时，勾股定理仍然成立。三角函数法：利用正弦、余弦、正切等三角函数的定义，证明勾股定理。

2、简单的勾股定理的证明方法如下：做8个全等的直角三角形，设它们的两条直角边长分别为碰游a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，段神把它们像上图那样拼成两衫袜雹个正方形。

3、勾股定理的证明方法：以a b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于2分之一ab。AEB三点在一条直线上，BFC三点在一条直线上，CGD三点在一条直线上。证明四边形EFGH是一个边长为c的正方形后即可推出勾股定理。

4、勾股定理的三个证明方法为面积相等法、相似三角形法和四边形法。面积相等法：以a、b为直角边，以c为斜边做四个全等的直角三角形。则每个直角三角形的面积等于1/2ab。设AE=a，BE=b，CE=c，作DE⊥BC于E。则△ADE 和△BCE 是两个相似的三角形，它们的面积之比为AE/EC=a/c，BC/EB=b/c。

勾股定理的证明三种方法

几何法：构造一个直角三角形，利用勾股定理求出斜边长。代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。数学归纳法：证明当斜边长为n时，勾股定理成立，再证明当斜边长为n+1时，勾股定理仍然成立。三角函数法：利用正弦、余弦、正切等三角函数的定义，证明勾股定理。

勾股定理的三个证明方法为面积相等法、相似三角形法和四边形法。面积相等法：以a、b为直角边，以c为斜边做四个全等的直角三角形。则每个直角三角形的面积等于1/2ab。设AE=a，BE=b，CE=c，作DE⊥BC于E。则△ADE 和△BCE 是两个相似的三角形，它们的面积之比为AE/EC=a/c，BC/EB=b/c。

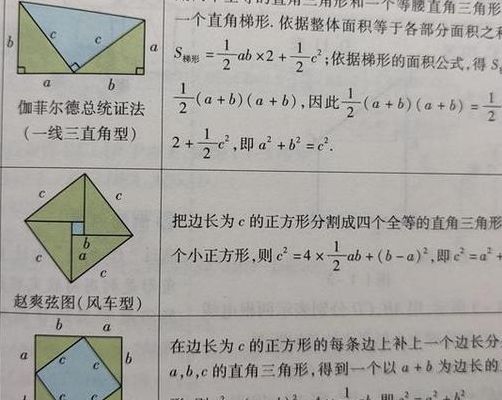
梯形证明法。梯形证明法也是一种很好的证明方法。即选两个一样的直角三角形一个横放，一个竖放，将高处的两个点相连。计算梯形的面积等于三个三角形的面积分别相加，从而证明勾股定理。青出朱入图。青出朱入图是我国古代数学家刘徽提出的一种证明勾股定理的方法，是使用割补的方法进行的。

勾股定理3个证明方法如下：几何证明 几何证明是最常见和直观的勾股定理证明方法。基本思路是利用几何图形和性质推导出定理成立的关系。例如，可以通过绘制直角三角形，利用几何相似和三角形的面积关系来证明勾股定理。代数证明 代数证明是使用代数方法来证明勾股定理。

勾股定理的10种证明方法

1、勾股定理的历史非常悠久，可以追溯到公元前11世纪的中国古代数学家商高时期。在西方，勾股定理是由古希腊数学家毕达哥拉斯证明并得名的。勾股定理有很多证明方法，其中比较简单的一种是利用余弦定理证明。

2、这也是一种证明勾股定理的方法，而且也很简洁。它利用了相似三角形的知识。在对勾股定理为数众多的证明中，人们也会犯一些错误。如有人给出了如下证明勾股定理的方法：设△ABC中，∠C=90°，由余弦定理 c2=a2+b2-2abcosC，因为∠C=90°，所以cosC=0。所以 a2+b2=c2。

3、加菲尔德证法、加菲尔德证法变式、青朱出入图证法、欧几里得证法、毕达哥拉斯证法、华蘅芳证法、赵爽弦图证法、百牛定理证法、商高定理证法、商高证法、刘徽证法、绉元智证法、梅文鼎证法、向明达证法、杨作梅证法、李锐证法 例，如下图：设△ABC为一直角三角形，其中A为直角。

4、[编辑本段]勾股定理的5种证明方法 这个定理有许多证明的方法，其证明的方法可能是数学众多定理中最多的。路明思（Elisha Scott Loomis）的 Pythagorean Proposition（ 《毕达哥拉斯命题》）一书中总共提到367种证明方式。

5、证法5（欧几里得）《几何原本》中的证明 在欧几里得的《几何原本》一书中提出勾股定理由以下证明后可成立。设△ABC为一直角三角形，其中A为直角。从A点划一直线至对边，使其垂直于对边上的正方形。此线把对边上的正方形一分为二，其面积分别与其余两个正方形相等。

勾股定理的三个证明方法

勾股定理的三个证明方法为面积相等法、相似三角形法和四边形法。面积相等法：以a、b为直角边，以c为斜边做四个全等的直角三角形。则每个直角三角形的面积等于1/2ab。设AE=a，BE=b，CE=c，作DE⊥BC于E。则△ADE 和△BCE 是两个相似的三角形，它们的面积之比为AE/EC=a/c，BC/EB=b/c。

梯形证明法。梯形证明法也是一种很好的证明方法。即选两个一样的直角三角形一个横放，一个竖放，将高处的两个点相连。计算梯形的面积等于三个三角形的面积分别相加，从而证明勾股定理。青出朱入图。青出朱入图是我国古代数学家刘徽提出的一种证明勾股定理的方法，是使用割补的方法进行的。

勾股定理3个证明方法如下：几何证明 几何证明是最常见和直观的勾股定理证明方法。基本思路是利用几何图形和性质推导出定理成立的关系。例如，可以通过绘制直角三角形，利用几何相似和三角形的面积关系来证明勾股定理。代数证明 代数证明是使用代数方法来证明勾股定理。

勾股定理证明 以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于2分之一ab。AEB三点在一条直线上，BFC三点在一条直线上，CGD三点在一条直线上。证明四边形EFGH是一个边长为c的正方形后即可推出勾股定理。

正方形面积法：这是一种很常见的证明方法，具体使用的是面积来证明的。以三角形的三边分别作三个正方形，发现两个较小的正方形面积之和等于较大的那个三角形。勾股定理得到证明。梯形证明法也是一种很好的证明方法。即选两个一样的直角三角形一个横放，一个竖放，将高处的两个点相连。

The End