格子乘法的规律（格子乘法的规律46x75）

意大利格子乘法的原理是什么?

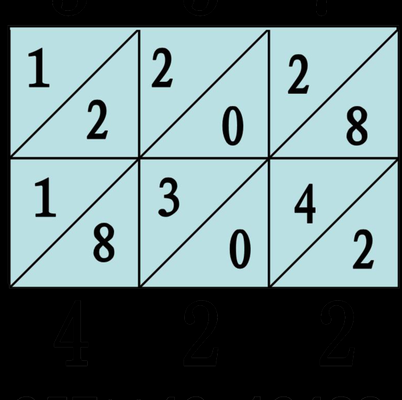
格子乘法是这样的，例如：计算乘积128×456，先画一个矩形，把它分成3×3个小格，在小格边上依次写下乘数、被乘数的各位数字。再用对角线把小格一分为二，分别记录上述各位数字相应乘积的十位数与个位数。

意大利格子的算法就是把每两个数字相乘的积写在它们对应的方格里。格子算法也叫铺地锦，是500多年前的意大利发现的一种数学算法，后来在明朝与笔算等同时传入中国，该算法需要用算筹一个个地列算出来，然后再相加。

“格子乘法”是15世纪中叶，意大利数学家帕乔利在《算术、几何及比例性质摘要》一书中介绍的一种两个数的相乘的计算方法。格子算法介于画线和算式之间。

然后，沿对角线求和以得到最终的乘积。旁边的注释指导了整个方法的操作。这种格子法是一种图形化的乘法计算方法，对于理解乘法的基本原理和步骤非常有帮助。

意大利格子乘法是一种手算乘法的方式，它通过在格子上逐行写下数字并匹配来计算乘积。将357写在格子的上方，将46写在格子的右侧。将357每一位数依次乘以4，并将每个乘积写在第一行的格子里。

格子乘法的计算方法是什么?

下图展示了格子乘法（或称为格子法）的计算方法。在第一个示例中，我们选择了两个数23和17进行乘法计算。通过创建一个网格并为每一对数字组合填充乘法结果，然后沿对角线求和，就可以得到最终的乘法结果。

每个格子的值等于其所在行和列的数的乘积。例如，第一个格子的值等于23乘以1（即23），第二个格子的值等于23乘以2（即46），以此类推。格子乘法不仅可以提高乘法的计算速度，还可以方便地进行误差检查和计算结果的核对。

先画一个矩形，把它分成m×n个方格（m，n分别为两乘数的位数），在方格上边、右边分别写下两个因数。再用对角线把方格一分为二，分别记录上述各位数字相应乘积的十位数与个位数。

格子乘法是15世纪中叶，意大利数学家帕乔利在《算术、几何及比例性质摘要》一书中介绍的一种两个数相乘的计算方法，格子算法介于画线和算式之间。

格子乘法的计算方法

1、格子乘法怎么算如下：先画一个矩形，把它分成m×n个方格（m，n分别为两乘数的位数），在方格上边、右边分别写下两个因数。再用对角线把方格一分为二，分别记录上述各位数字相应乘积的十位数与个位数。

2、下图展示了格子乘法（或称为格子法）的计算方法。在第一个示例中，我们选择了两个数23和17进行乘法计算。通过创建一个网格并为每一对数字组合填充乘法结果，然后沿对角线求和，就可以得到最终的乘法结果。

3、每个格子的值等于其所在行和列的数的乘积。例如，第一个格子的值等于23乘以1（即23），第二个格子的值等于23乘以2（即46），以此类推。格子乘法不仅可以提高乘法的计算速度，还可以方便地进行误差检查和计算结果的核对。

4、将格子中的所有数字加起来，得到最终的乘积。在这个例子中，我们将所有的数字加起来得到648。这就是格子乘法的全部过程。通过这种方法，孩子们可以亲手用图形表示出每一个乘积，更好地理解乘法运算的过程。

5、基本乘法：要计算两个单元格中的数字的乘积，可以使用以下公式：=A1*B1这将返回单元格A1和B1中数字的乘积。连续乘法：如果要计算多个数字的连续乘积，可以继续使用乘法运算符。

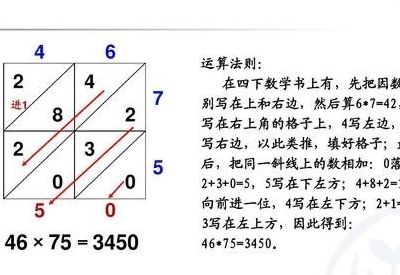
6、格子乘法计算过程小学四年级上册人教版数学书57页中介绍了格子乘法，比如用该方法计算（46*75）的过程是：1）因为是两位数乘两位数，就画一个2*2的格子图，如果是m位数乘n位数，就画一个m*n的格子图。

格子乘法的原理是什么?

1、格子乘法是这样的，例如：计算乘积128×456，先画一个矩形，把它分成3×3个小格，在小格边上依次写下乘数、被乘数的各位数字。再用对角线把小格一分为二，分别记录上述各位数字相应乘积的十位数与个位数。

2、纳皮尔尺可以用加法和乘法代替多位数的乘法，也可以用除数为一位数的除法和减法代替多位数除法，从而简化了计算。纳皮尔尺的计算原理是“格子乘法”。

3、方法如下：“格子乘法”的原理是先画一个矩形，根据两个乘数的位数，将其分为对应的位数位数的小格。 在小格的边缘依次写乘数、被乘数的各位数字，用对角线将小格分成两部分，分别记录与上述各位数字对应的积的10位和1位。

15世纪意大利的一本算数书中介绍了一种“格子乘法”。你能仿照右面的...

“格子乘法”是15世纪中叶，意大利数学家帕乔利在《算术、几何及比例性质摘要》一书中介绍的一种两个数的相乘的计算方法。格子算法介于画线和算式之间。

拉普拉斯和拉格朗日是19世纪初法国的两位数学家。拉普拉斯在数学上十分伟大，在政治上却是一个十足的小人，每次政权更迭，他都能够见风使舵，毫无政治操守可言。拉普拉斯曾把他的巨著《天体力学》献给拿破仑。

*37=15725 “格子乘法”是15世纪中叶，意大利数学家帕乔利在《算术、几何及比例性质摘要》一书中介绍的一种两个数的相乘的计算方法。

The End