勾股定理各种证明方法（勾股定理的证明方法24种）

勾股定理5种证明方法

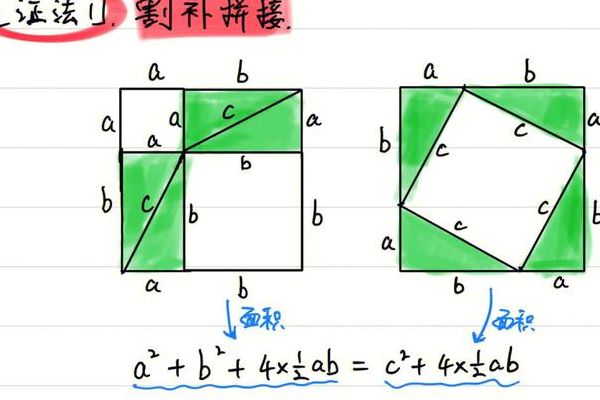
证法1 做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形这两个正方形的边长都是a+b，所以面积相等。

勾股定理证明方法有：正方形面积法、赵爽弦图验证法、梯形证明法、欧几里得证明法、面积割补法等。

相似三角形法：利用相似三角形的性质，证明勾股定理。矩形法：将一个直角三角形内切于一矩形中，从而证明勾股定理。差积公式法：利用差积公式（a+b）（a-b）=a-b，证明勾股定理。

我国历代数学家关于勾股定理的论证方法有多种，为勾股定理作的图注也不少，其中较早的是赵爽（即赵君卿）在他附于《周髀算经》之中的论文《勾股圆方图注》中的证明。

勾股定理5种证明方法如下：几何法证明：使用几何图形的性质来证明勾股定理。应用勾股定理法证明：使用已知的勾股定理来证明勾股定理。斜率法证明：使用斜率的定义来证明勾股定理。

验证勾股定理的五种方法如下：勾股定理的验证是：赵爽“弦图”验证法、欧几里得证明勾股定理、面积割补验证法。赵爽“弦图”验证法 赵爽“弦图”是一种利用平面几何图形来验证勾股定理的方法。

勾股定理的多种证明方法

勾股定理现发现约有400种证明方法，是数学定理中证明方法最多的定理之一。勾股数是组成a+b=c的正整数组(a，b，c)。(3，4，5)就是勾股数。

几何法：构造一个直角三角形，利用勾股定理求出斜边长。代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。

勾股定理证明方法有：正方形面积法、赵爽弦图验证法、梯形证明法、欧几里得证明法、面积割补法等。

注意“案”中的“弦图又可以”、“亦成弦实”，“又”“亦”二字表示赵爽认为勾股定理还可以用另一种方法证明，于是他给出了新的证明。

勾股定理的证明方法最简单的6种如下：正方形面积法 这是一种很常见的证明方法，具体使用的是面积来证明的。以三角形的三边分别作三个正方形，发现两个较小的正方形面积之和等于较大的那个三角形。勾股定理得到证明。

欧拉定理证明法。构造出一个直角三角形，把它的两条直角边对应的两个正方形放在真角三角形外面，另一条边对应的正方形放在直角三角形内部。再利用欧拉定理计算出三个正方形的面积，可以证明勾股定理。代数证明法。

勾股定理的16种证明法

1、证法十二（利用多列米定理证明）；1证法十四（利用反证法证明）；1证法十五（辛卜松证明）；1证法十六（陈杰证明）。

2、第一种方法：边长为的正方形可以看作是由4个直角边分别为a、b，斜边为c 的直角三角形围在外面形成的。

3、勾股定理的证明方法如下：证法一。以a、b为直角边，以c为斜边做四个全等的三角形，按下图所示相拼，使A、E、B三点共线，B、F、C三点共线，C、G、D三点共线。

勾股定理的常见三种证明方法

青朱出入图 青朱出入图，是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法，特色鲜明、通俗易懂。欧几里得证法 在欧几里得的《几何原本》一书中给出勾股定理的以下证明。

证法十一(利用切割线定理证明)： 在直角三角形ABC中，∠ACB=90°，AC=b，AB=c，BC=a，以B为圆心，a为半径画圆，AB交圆与D点，AB的延长线交圆于E点。

勾股定理的三个证明方法为面积相等法、相似三角形法和四边形法。面积相等法：以a、b为直角边，以c为斜边做四个全等的直角三角形。则每个直角三角形的面积等于1/2ab。设AE=a，BE=b，CE=c，作DE⊥BC于E。

The End