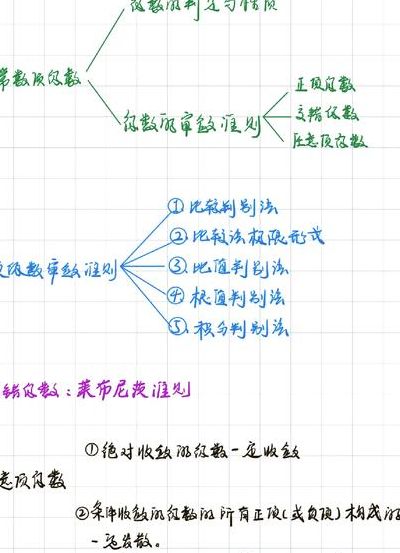
级数收敛的判别方法（正项级数收敛的判别方法）

判断级数收敛的方法总结

a1，当n趋于无穷，a^n趋于0，一般项1/(1+a^n)趋于1，级数发散。a=1 一般项1/(1+a^n)=1/2，级数发散。a1， 1/(1+a^n)1/a^n。因为1/a1，级数1/a^n收敛，原级数收敛。所以：a1收敛，0a1，级数发散。

判定正项级数的敛散性；判定交错级数的敛散性；求幂级数的收敛半径、收敛区间和收敛域；求幂级数的和函数与数项级数的和；将函数展开为傅里叶级数。判定正项级数的敛散性先看当n趋向于无穷大时，级数的通项是否趋向于零（如果不易看出，可跳过这一步）。

比较判别法比较判别法是判断级数收敛的一种常用方法。如果级数∑an的每一项都是非负数，可以将其与一个已知的收敛级数∑bn进行比较，如果bn≥an，则级数∑an收敛；如果bn≤an，则级数∑an发散；如果无法比较，则比较判别法无法判断。比值判别法比值判别法是判断级数收敛的另一种常用方法。

首先，拿到一个数项级数，先判断其是否满足收敛的必要条件：若数项级数收敛，则 n→+∞ 时，级数的一般项收敛于零。（这一必要条件一般用于证明级数的发散性，即一般项不收敛于零。）若满足其必要性。

此外，根值判别法也是判断级数收敛性的一种有效手段。该方法需要取级数每一项的绝对值开n次方，并求其极限值。如果这个极限值小于1，则级数收敛；如果大于1，则级数发散。积分判别法则是另一种常见的方法，它将待判断的级数转化为函数的积分形式，通过判断积分是否收敛来确定级数的收敛性。

如何判断一个级数是不是收敛的?

所以：a1收敛，0a1，级数发散。

比较判别法：如果P级数与另一个已知收敛或发散的级数相比，可以得到其收敛性。例如，当p1时，P级数收敛；当0极限比较法：通过计算P级数的极限值，可以判断其收敛性。如果极限值为有限数，则P级数收敛；如果极限值为无限大或无限小，则P级数发散。

证明方法一：un=1/n是个正项级数，从第二项开始1/n＜1/（n-1）n=1/（n-1）-1/n 所以这个级数是收敛的。证明方法二：lim(1/n*tan1/n)/(1/n^2)=lim(tan1/n)/(1/n)=1；所以1/n*tan1/n与1/n^2敛散性相同，1/n^2收敛，所以原级数收敛。

轮换级数测试（Alternating Series Test）：如果一个级数的项交替变号，并且每一项的绝对值都在减小并趋于零，那么这个级数是收敛的。积分测试：如果一个函数在一个区间上可积，并且对应的不定积分收敛，那么对应的级数也是收敛的。

cocrni中熵合金

为克服传统工艺的挑战，逯文君研究员团队在LPBF技术基础上，发展出一项创新的原位合金化策略，成功制备出强韧的CoCrNi/Cr2B复合材料。通过在CoCrNi中熵合金基体中添加1 wt.%的B4C颗粒，促使硼化物在LPBF过程中原位生成，形成独特的核壳结构，优化了复合材料的力学性能。

该研究通过双粉末源合金体系，包括CoCrNi中熵合金与添加了单质Ti和Al的相同MEA（CoCrNi合金中加入Al7Ti7），实现层状异质结构的交替沉积，并在非破坏性热处理后，获得了协同强度-延展性的优异性能，极限抗拉强度超过1GPa，延展性接近50%。此合金体系在强度-延展性优值方面，优于报道的其他中/高熵合金。

他们的研究成果被顶级期刊《Composites Part B： Engineering》收录，标志着该研究在增材制造领域取得了重要突破。开发出高强韧中熵合金复合材料：研究团队与南京理工大学朱志光教授合作，成功开发出一种通过激光粉末床熔融技术制备的高强韧中熵合金复合材料——CoCrNi/Cr2B。

研究团队与南京理工大学朱志光教授合作，成功开发出一种通过激光粉末床熔融技术LPBF制备的高强韧中熵合金复合材料——CoCrNi/Cr2B。

The End