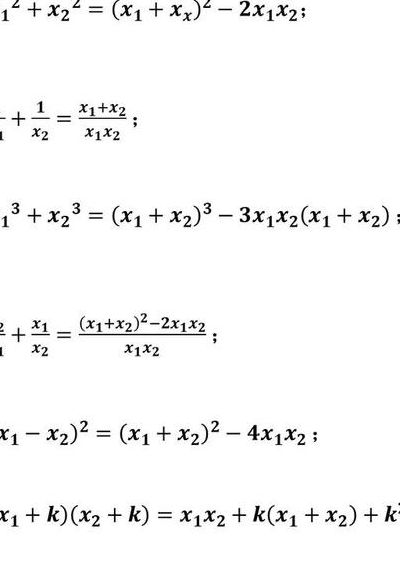韦达定理所有公式（韦达定理所有公式变形）

高中韦达定理共有多少变形公式?

1、高中韦达定理8个变形公式如下：向量共线公式：如果向量a、b、c共线，则有a×b+b×c+c×a=0。意思是如果三个向量共线，那么它们的叉积和为0。向量平行公式：如果向量a、b平行，则有a×b=0。意思是如果两个向量平行，那么它们的叉积为0。

2、韦达定理变形公式10个都有x1+x2=-b/a， x1x2=c/a。x1+x2=(x1+x2)-2x1x2，1/x1+1/x2=(x1+x2)/x1x2，x1+x2=(x1+x2)(x1-x1x2+x2)等。

3、韦达定理变形公式有：韦达定理公式变形：x1+x2=(x1+x2)-2x1x2。1/x1+1/x2=(x1+x2)/x1x2。x1+x2=(x1+x2)(x1-x1x2+x2)。

三次函数的韦达定理怎么推导出来的?

1、三次函数的韦达定理公式如下：y=ax+bx+cx+d（a≠0，b、c、d为常数）。韦达定理是指一元二次方程中根和系数之间的关系。韦达定理解析 法国数学家弗朗索瓦·韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理。

2、韦达定理的推导过程如下 韦达定理说明了一元二次方程中根和系数之间的关系。法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理。由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理。

3、韦达定理三次方程是aX^3+bX^2+cX+d=0。解法思想 三次方程是未知项总次数最高为3的整式方程，其解法思想是通过配方和换元，使三次方程降次为二次方程。

韦达定理三个公式

1、韦达定理的三个公式为： 对于一元二次方程ax+bx+c=0 (a0)，若其两个根为x和x，则x+x=-b/a。 一元二次方程ax+bx+c=0 (a0)的两个根x和x的积为xx=c/a。

2、一元n次方程韦达定理公式有和根、乘积根、交叉乘积。和根（Sum of Roots）：所有根的和等于负数b/a，即[x_1+x_2+x_3+\ldots+x_n=-\frac{b}{a}]。乘积根（Product of Roots）：所有根的乘积等于k/a，即[x_1\cdot x_2\cdot x_3\cdot\ldots\cdot x_n=\frac{k}{a}]。

3、韦达定理公式变形：x1+x2=(x1+x2)-2x1x2。1/x1+1/x2=(x1+x2)/x1x2。x1+x2=(x1+x2)(x1-x1x2+x2)。

4、韦达定理三个公式如下：根的和公式：若一元二次方程为ax^2+bx+ c=0，则两根之和为-b/a。这个公式表示一元二次方程的两个根的和等于二次项系数与一次项系数之比的负值。这是因为一元二次方程可以表示为两个一次方程的乘积，即（x-α）（x-β）=0，其中α和β是方程的两个根。

5、韦达定理的三个公式是：X1+X2=-b/a，X1×X2=c/a，△=b^2-4ac，韦达定理说明了一元二次方程中根和系数之间的关系，可以利用两数的和积关系构造一元二次方程。韦达定理的推导过程：ax+bx+c=0（a、b、c为实数且a≠0）中，由一元二次方程求根公式可知：X2。

6、x1*x2+x2*x3+x3*x1=c/a x1*x2*x3=-d/a 韦达定理介绍 韦达定理又称作角平分线定理，是解析几何中非常重要的定理之一，它极大地简化了一些几何问题的求解过程。

韦达定理的公式有什么?

1、韦达定理的7个公式为： 根系关系公式：如果一元二次方程ax+bx+c=0的根为α和β，那么α+β=-b/a，αβ=c/a。 根与系数的关系公式：对于任意一元二次方程ax+bx+c=0，有α^3 + β^3 = ^3 - 3αβ = -b^3/a^3等。还有其他关于根的和与积的公式。

2、高中韦达定理8个变形公式如下：向量共线公式：如果向量a、b、c共线，则有a×b+b×c+c×a=0。意思是如果三个向量共线，那么它们的叉积和为0。向量平行公式：如果向量a、b平行，则有a×b=0。意思是如果两个向量平行，那么它们的叉积为0。

3、韦达定理变形公式10个都有x1+x2=-b/a， x1x2=c/a。x1+x2=(x1+x2)-2x1x2，1/x1+1/x2=(x1+x2)/x1x2，x1+x2=(x1+x2)(x1-x1x2+x2)等。

4、韦达定理公式：ax^2+bx+c=0x=(-b±√(b^2-4ac))/2ax1+x2=-b/a x1x2=c/a。达定理说明了一元二次方程中根和系数之间的关系。

The End