高中正态分布三个公式（高中正态分布视频讲解）

高中正态分布相关公式有哪些?

1、高中正态分布的三个重要公式是： 正态分布函数的概率密度函数：在一维情况下，正态分布的概率密度函数可以表示为：f(x) = 1 / (σ * √(2π)) * e^(-((x-μ)^2)/(2σ^2))其中，f(x)表示随机变量X在某个特定取值x处的概率密度，μ表示分布的均值（期望值），σ表示分布的标准差。

2、正态分布三个公式 横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%，横轴区间（μ-58σ，μ+58σ）内的面积为9730020%。X~N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ-σ）。

3、在高中统计学中，我们通常使用正态分布来描述连续型的随机变量。正态分布有三个常用的公式： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数是一个关于变量 x 的函数，表示了变量取某个值的概率密度。

4、正态分布公式如图所示：正态分布是具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ，σ^2 )。

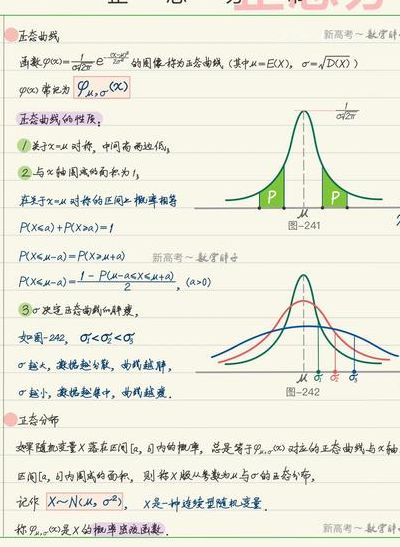
5、如果函数为φμ，σ(x)= 12πσ e？(x？μ)22σ2，x∈(？∞，+∞)，其中实数μ和σ(σ0)为参数。我们称φμ，σ(x)的图象为正态分布密度曲线，简称正态曲线。

正态分布概率公式三个

高中正态分布的三个重要公式是： 正态分布函数的概率密度函数：在一维情况下，正态分布的概率密度函数可以表示为：f(x) = 1 / (σ * √(2π)) * e^(-((x-μ)^2)/(2σ^2))其中，f(x)表示随机变量X在某个特定取值x处的概率密度，μ表示分布的均值（期望值），σ表示分布的标准差。

在高中统计学中，我们通常使用正态分布来描述连续型的随机变量。正态分布有三个常用的公式： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数是一个关于变量 x 的函数，表示了变量取某个值的概率密度。

在统计学中，正态分布（也称为高斯分布）是一种常见的概率分布。

正态分布概率公式三个是：974%、945%、627%，正态分布（Normaldistribution），也称“常态分布”，又名高斯分布（Gaussiandistribution），最早由棣莫弗（AbrahamdeMoivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。

高中正态分布三个公式是：横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%。横轴区间（μ－58σ，μ＋58σ）内的面积为9730020%。X-N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ－σ）。

高中正态分布三大公式

高中正态分布的三个重要公式是： 正态分布函数的概率密度函数：在一维情况下，正态分布的概率密度函数可以表示为：f(x) = 1 / (σ * √(2π)) * e^(-((x-μ)^2)/(2σ^2))其中，f(x)表示随机变量X在某个特定取值x处的概率密度，μ表示分布的均值（期望值），σ表示分布的标准差。

正态分布三个公式 横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%，横轴区间（μ-58σ，μ+58σ）内的面积为9730020%。X~N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ-σ）。

在高中统计学中，我们通常使用正态分布来描述连续型的随机变量。正态分布有三个常用的公式： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数是一个关于变量 x 的函数，表示了变量取某个值的概率密度。

正态分布公式如图所示：正态分布是具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ，σ^2 )。

φ(X)=12πe？x22，x∈(？∞，+∞)，那么称X服从标准正态分布，即X~N（0，1）。3σ原则 若X~N（μ，σ2），则对于任何实数a0，P(μ？aX≤μ+a)=∫μ？aμ+aφμ，σ(x)dx。正态总体几乎总取值于区间(μ？3σ，μ+3σ)之内。

请问正态分布相关的三个重要公式是什么?

1、[CLASSIC] 正态分布是统计学中最重要且最常用的连续概率分布之一。它可以用以下三个常用的公式来描述： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数通常用符号 φ(x) 表示。

2、高中正态分布的三个重要公式是： 正态分布函数的概率密度函数：在一维情况下，正态分布的概率密度函数可以表示为：f(x) = 1 / (σ * √(2π)) * e^(-((x-μ)^2)/(2σ^2))其中，f(x)表示随机变量X在某个特定取值x处的概率密度，μ表示分布的均值（期望值），σ表示分布的标准差。

3、高中正态分布三个公式是：横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%。横轴区间（μ－58σ，μ＋58σ）内的面积为9730020%。X-N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ－σ）。

4、正态分布三个公式 横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%，横轴区间（μ-58σ，μ+58σ）内的面积为9730020%。X~N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ-σ）。

5、若（）X～N（μ，σ2），则X的均值与方差分别为：E(X)=μ，D(X)=σ2。标准正态分布 如果随机变量X的概率函数为 φ(X)=12πe？x22，x∈(？∞，+∞)，那么称X服从标准正态分布，即X~N（0，1）。

正态分布的三个公式是什么?

在高中统计学中，我们通常使用正态分布来描述连续型的随机变量。正态分布有三个常用的公式： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数是一个关于变量 x 的函数，表示了变量取某个值的概率密度。

高中正态分布的三个重要公式是： 正态分布函数的概率密度函数：在一维情况下，正态分布的概率密度函数可以表示为：f(x) = 1 / (σ * √(2π)) * e^(-((x-μ)^2)/(2σ^2))其中，f(x)表示随机变量X在某个特定取值x处的概率密度，μ表示分布的均值（期望值），σ表示分布的标准差。

在统计学中，正态分布（也称为高斯分布）是一种常见的概率分布。

高中正态分布三个公式是：横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%。横轴区间（μ－58σ，μ＋58σ）内的面积为9730020%。X-N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ－σ）。

正态分布三个公式 横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%，横轴区间（μ-58σ，μ+58σ）内的面积为9730020%。X~N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ-σ）。

高中正态分布三个公式是什么?

1、正态分布三个公式 横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%，横轴区间（μ-58σ，μ+58σ）内的面积为9730020%。X~N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ-σ）。

2、高中正态分布三个公式是：横轴区间（μ-σ，μ+σ）内的面积为6268949%，横轴区间（μ-96σ，μ+96σ）内的面积为9449974%。横轴区间（μ－58σ，μ＋58σ）内的面积为9730020%。X-N(μ，σ)：一般正态分布：均值为μ、方差为σP(μ－σ）。

3、正态分布公式如图所示：正态分布是具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N(μ，σ^2 )。

4、在高中统计学中，我们通常使用正态分布来描述连续型的随机变量。正态分布有三个常用的公式： 概率密度函数（Probability Density Function， PDF）：正态分布的概率密度函数是一个关于变量 x 的函数，表示了变量取某个值的概率密度。

5、若（）X～N（μ，σ2），则X的均值与方差分别为：E(X)=μ，D(X)=σ2。标准正态分布 如果随机变量X的概率函数为 φ(X)=12πe？x22，x∈(？∞，+∞)，那么称X服从标准正态分布，即X~N（0，1）。

The End