分段函数的定义域（分段函数的定义域求法）

分段函数的定义域怎么求

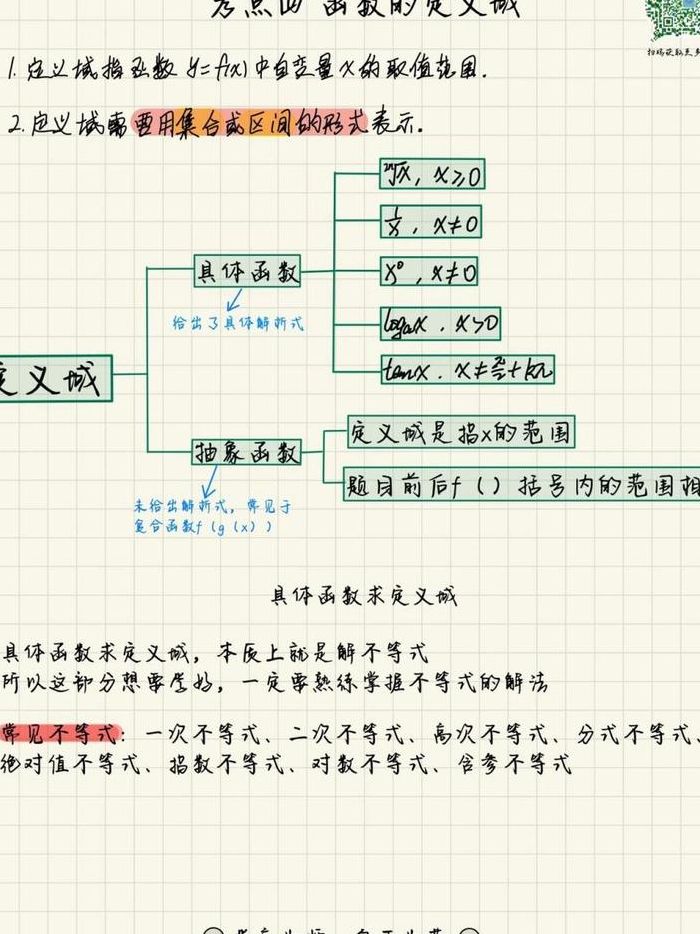
求函数的定义域的依据就是要使函数的解析式有意义的自变量的取值范围。其求解根据一般有：分式中，分母不为零；偶次根式中，被开方数非负；对数的真数大于0。

求分段函数的定义域，我们可以按照以下步骤来操作：分别考虑每一段：把分段函数拆分成几个独立的函数段，每段看作一个“小函数”。根据规则求定义域：对于分式部分，要保证分母不为零。对于偶次根式部分，要保证被开方数非负。对于对数部分，要保证真数大于0。

确定每一段函数的定义域：需要分析分段函数中每一段函数的形式，确定其各自的定义域。如某一段是一个分式，分母不能为零；某一段含有平方根，被开方数必须非负；某一段涉及对数，对数的真数必须大于零。

分段函数的定义域

1、分段函数的定义域是指将各个分段函数的定义域取并集得到的集合。每个分段函数的定义域是指函数中自变量可以取的值的集合，这些值必须使得函数的解析式有意义。求解分段函数的定义域通常需要遵循以下原则： 分式中分母不为零。 偶次根式中被开方数非负。 对数的真数大于零。

2、分段函数的定义域是各段函数定义域的并集。定义域是函数的三要素(定义域、值域、对应法则)之一，对应法则的作用对象。指函数自变量的取值范围，即对于两个存在函数对应关系的非空集合D、M，集合D中的任意一个数，在集合M中都有且仅有一个确定的数与之对应，集合D称为函数定义域。

3、分段函数的定义域是各段函数定义域的并集，所以所求定义域为 {x｜x=0}∪{x｜x≠0}=R，即定义域为全体实数。

4、分段函数定义域等于各段x的范围的并集。各段x的范围不能重复的。

非结构化数据如何可视化呈现？

按图像数据可视化：使用具有真实含义的图像和图标，使数据和图表更加逼真，易于理解。示例包括男性和女性图标的比例显示。 通过概念实现数据可视化：将抽象的指标数据转换为熟悉且易于理解的数据，以形象地解释概念。示例包括非结构化数据的解释和信息图。

信息可视化 信息可视化是一个跨学科领域，其核心在于利用视觉呈现手段来处理大规模的非数值型信息资源。这包括了软件系统中的文件、程序代码等复杂信息集合，以及抽象数据集如非结构化文本、高维空间中的点等。

首先，数据是可视化的基础。可视化是用图形、图表、仪表盘等视觉形式来呈现数据，因此需要有数据作为可视化的对象。数据可以是定量数据或定性数据，可以是结构化的或非结构化的，可以是单一变量或多变量数据。数据的质量、特征和分布都会影响可视化的效果和解释。其次，设计是可视化的关键。

信息可视化（Information visualization）则是一个跨学科领域，主要研究大规模非数值信息资源的视觉呈现。信息可视化侧重于帮助人们理解和分析数据，特别是在处理软件系统中的大量非数值型信息时更为有效。例如，软件系统中的文件、程序代码等，以及非结构化文本或高维空间中的点等数据集。

数据存储 数据预处理之后，下一个问题就是：数据该如何进行存储？通常大家最为熟知是MySQL、Oracle等传统的关系型数据库，它们的优点是能够快速存储结构化的数据，并支持随机访问。

息可视化（Informationvisualization）是一个跨学科领域，旨在研究大规模非数值型信息资源的视觉呈现（如软件系统之中众多的文件或者一行行的程序代码）。通过利用图形图像方面的技术与方法，帮助人们理解和分析数据。

分段函数定义域怎么求

确定每一段函数的定义域：需要分析分段函数中每一段函数的形式，确定其各自的定义域。如某一段是一个分式，分母不能为零；某一段含有平方根，被开方数必须非负；某一段涉及对数，对数的真数必须大于零。

求分段函数的定义域，我们可以按照以下步骤来操作：分别考虑每一段：把分段函数拆分成几个独立的函数段，每段看作一个“小函数”。根据规则求定义域：对于分式部分，要保证分母不为零。对于偶次根式部分，要保证被开方数非负。对于对数部分，要保证真数大于0。

求函数的定义域的依据就是要使函数的解析式有意义的自变量的取值范围。其求解根据一般有：分式中，分母不为零；偶次根式中，被开方数非负；对数的真数大于0。

分段函数的定义域是各段函数定义域的并集，所以所求定义域为 {x｜x=0}∪{x｜x≠0}=R，即定义域为全体实数。

The End